Carl Friedrich Gauss
Johann Carl Friedrich Gauss (/ɡaʊs/; German: Gauß [ˈkaʁl ˈfʁiːdʁɪç ˈɡaʊs] (![]() lisen);[1][2] Latin: Carolus Fridericus Gauss; 30 April 1777 – 23 February 1855) was a German mathematishan and fizisist hoo maed significant contribueshuns to meny feelds in mathematics and sieens.[3] Sumtiems referd to as th Princeps mathematicorum[4] (Latin for '"th formoest of mathematicians"') and "th graetest mathematishan sinss antiqity", Gauss had an exsepshunal inflooens in meny feelds of mathematics and sieens, and is rankt amung history's moest inflooenshal mathematicians.[5]
lisen);[1][2] Latin: Carolus Fridericus Gauss; 30 April 1777 – 23 February 1855) was a German mathematishan and fizisist hoo maed significant contribueshuns to meny feelds in mathematics and sieens.[3] Sumtiems referd to as th Princeps mathematicorum[4] (Latin for '"th formoest of mathematicians"') and "th graetest mathematishan sinss antiqity", Gauss had an exsepshunal inflooens in meny feelds of mathematics and sieens, and is rankt amung history's moest inflooenshal mathematicians.[5]
Bieografy[edit]
Erly yeers[edit]

Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in th Duchy of Brunswick-Wolfenbüttel (now part of Loeer Saxony, Germany), to pur, werking-clas pairents.[6] His muther was iliteret and never recorded th daet of his berth, remembering oenly that he had bin born on a Wednesday, aet days befor th Feest of th Ascension (which ocurs 39 days after Easter). Gauss laeter solvd this puzl about his berthdaet in th context of fiending th daet of Easter, derieving methods to compuet th daet in boeth past and fuecher yeers.[7] He was crisend and confermd in a cherch neer th scool he atended as a chield.[8]
Gauss was a chield prodijy. In his memorial on Gauss, Wolfgang Sartorius von Waltershausen sez that when Gauss was bairly three yeers oeld he corected a math error his faather maed; and that when he was seven, he confidently solvd an arrithmetic seerys problem (comonly sed to be 1 + 2 + 3 + ... + 98 + 99 + 100) faster than enywun els in his clas of 100 stoodents.[9] Meny verzhuns of this story hav bin re-toeld sinss that tiem with vairius deetaels regarding whut th seerys was – th moest freeqent being th clasical problem of ading all th intejers frum 1 to 100.[10][11][12] Thair ar meny uther anecdoets about his precosity whiel a todler, and he maed his ferst groundbreaking mathematical discuverys whiel stil a teenaejer. He compleeted his magnum oepus, Disquisitiones Arithmeticae, in 1798, at th aej of 21—tho it was not publisht until 1801.[13] This werk was fundamental in consolidaeting number theeory as a disiplin and has shaept th feeld to th prezent day.
Gauss's intelekchual abilitys atracted th atenshun of th Duek of Brunswick,[10][5] hoo sent him to th Coleejium Carolinum (now Braunschweig Ueniversity of Tecnolojy),[10] which he atended frum 1792 to 1795,[14] and to th Ueniversity of Göttingen frum 1795 to 1798.[13] Whiel at ueniversity, Gauss independently re-discuverd several important theorems.[15] His braekthroo ocurd in 1796 when he shoed that a reguelar polygon can be constructed bi compas and straet-ej if th number of its sieds is th product of distinkt Fermat priems and a power of 2.[a] This was a maejor discuvery in an important feeld of mathematics; construcshun problems had ocuepied mathematicians sinss th days of th Aenshent Greeks, and th discuvery ultimetly led Gauss to chooz mathematics insted of filolojy as a career. Gauss was so pleezd with this rezult that he reqested that a reguelar heptadecagon be inscriebd on his toomstoen. Th stoenmaeson decliend, staeting that th dificult construcshun wuud esenshaly luuk liek a sercl.[16]
Th yeer 1796 was productiv for boeth Gauss and number theeory. He discuverd a construcshun of th heptadecagon on 30 March.[13][17] He ferther advanst mojular arrithmetic, graetly simplifying manipuelaeshuns in number theeory. On 8 April he becaem th ferst to proov th qodratic reciprocity law. This remarkably jeneral law alows mathematicians to determin th solvability of eny qodratic eqaezhun in mojular arrithmetic. Th priem number theeorem, conjekcherd on 31 May, givs a guud understanding of how th priem numbers ar distribueted amung th intejers.
Gauss allso discuverd that evry pozitiv intejer is representable as a sum of at moest three tri-angguelar numbers on 10 July and then joted doun in his dieery th noet: "ΕΥΡΗΚΑ! num = Δ + Δ' + Δ". On 1 October he publisht a rezult on th number of solooshuns of polynoemials with co-efishents in fieniet feelds, which 150 yeers laeter led to th Weil conjekchers.
Laeter yeers and deth[edit]
Gauss remaend mentaly activ into his oeld aej, eeven whiel sufering frum gout and jeneral unhapynes.[18] For exampl, at th aej of 62, he taut himself Russian.[18]
In 1840, Gauss publisht his inflooenshal Dioptrische Untersuchungen,[19] in which he gaev th ferst sistematic analisis on th formaeshun of imejes under a paraxial aproximaeshun (Gaussian optics).[20] Amung his rezults, Gauss shoed that under a paraxial aproximaeshun an optical sistem can be carracteriezd bi its cardinal points[21] and he derievd th Gaussian lenz formuela.[22]
In 1845, he becaem an asoeshiaeted member of th Royal Instituet of th Netherlands; when that becaem th Royal Netherlands Academy of Arts and Sieenses in 1851, he joind as a forin member.[23]
In 1854, Gauss selected th topic for Bernhard Riemann's inaugueral lekcher "Über die Hypothesen, welche der Geometrie zu Grunde liegen" (About th hiepothesys that underli Jeometry).[24] On th way hoem frum Riemann's lekcher, Weber reported that Gauss was fuul of praez and exsietment.[25]
On 23 February 1855, Gauss died of a hart atak in Göttingen (then Kingdom of Hanover and now Loeer Saxony);[6][18] he is interd in th Albani Semeterry thair. Too peepl gaev eulogies at his fueneral: Gauss's sun-in-law Heinrich Ewald, and Wolfgang Sartorius von Waltershausen, hoo was Gauss's cloez frend and bieografer. Gauss's braen was prezervd and was studyd bi Rudolf Wagner, hoo found its mas to be slietly abuv averej, at 1,492 grams, and th serrebral airia eeqal to 219,588 sqair millimeters[26] (340.362 sqair inches). Hiely developt convolutions wer allso found, which in th erly 20th senchery wer sugjested as th explanaeshun of his jeenius.[27]
Relijus vues[edit]
Gauss was a Lutheran Protestant, a member of th St. Albans Evanjelical Lutheran cherch in Göttingen.[28] Potenshal evidens that Gauss beleevd in God cums frum his respons after solving a problem that had preeviusly defeeted him: "Fienaly, too days ago, I sucseeded—not on acount of mi hard eforts, but bi th graes of th Lord."[29] Wun of his bieografers, G. Waldo Dunnington, descriebd Gauss's relijus vues as foloes:
For him sieens was th meens of expoezing th imortal nueclius of th hueman soel. In th days of his fuul strength, it fernisht him recreaeshun and, bi th prospects which it oepend up to him, gaev consolaeshun. Tord th end of his lief, it braut him confidens. Gauss's God was not a coeld and distant figment of metafizics, nor a distorted carricachur of embiterd theolojy. To man is not vouchsafed that fuulnes of nolej which wuud warant his arrogantly hoelding that his blerd vizhun is th fuul liet and that thair can be nun uther which miet report th trooth as duz his. For Gauss, not he hoo mumbles his creed, but he hoo lievs it, is acsepted. He beleevd that a lief werthily spent heer on erth is th best, th oenly, preparaeshun for heven. Relijon is not a qeschun of literachur, but of lief. God's revelaeshun is continueus, not contaend in tablets of stoen or saecred parchment. A buuk is inspierd when it inspiers. Th unshakeable iedeea of personal continueans after deth, th ferm beleef in a last reguelaetor of things, in an eternal, just, omnishent, omnipotent God, formd th baesis of his relijus lief, which harmonized compleetly with his sieentific reserch.[30]
Apart frum his corespondens, thair ar not meny noen deetaels about Gauss's personal creed. Meny bieografers of Gauss disagree about his relijus stans, with Bühler and uthers considering him a deeist with verry unorthodox vues,[31][32][33] whiel Dunnington (tho admiting that Gauss did not beleev literaly in all Christian daugmas and that it is unnoen whut he beleevd on moest doctrinal and confeshunal qeschuns) points out that he was, at leest, a nominal Lutheran.[b]
In conecshun to this, thair is a record of a conversaeshun between Rudolf Wagner and Gauss, in which thay discust William Whewell's buuk Of th Plurality of Werlds. In this werk, Whewell had discarded th posibility of existing lief in uther planets, on th baesis of theolojical arguements, but this was a pozishun with which boeth Wagner and Gauss disagreed. Laeter Wagner explaend that he did not fuuly beleev in th Biebl, tho he confest that he "envyd" thoes hoo wer aebl to eezily beleev.[31][c] This laeter led them to discus th topic of faeth, and in sum uther relijus remarks, Gauss sed that he had bin mor inflooenst bi theoloejans liek Lutheran minister Paul Gerhardt than bi Moses.[34] Uther relijus inflooenses inclooded Wilhelm Braubach, Johann Peeter Süssmilch, and th Nue Testament. Too relijus werks which Gauss red freeqently wer Braubach's Seelenlehre (Giessen, 1843) and Süssmilch's Gottliche (Ordnung gerettet A756); he allso devoeted considerabl tiem to th Nue Testament in th orijinal Greek.[35]
Dunnington ferther elaboraets on Gauss's relijus vues bi rieting:
Gauss's relijus conshusnes was baest on an insaeshabl therst for trooth and a deep feeling of justis extending to intelekchual as wel as mateerial guuds. He conseevd spirichual lief in th hoel uenivers as a graet sistem of law penetraeted bi eternal trooth, and frum this sors he gaend th ferm confidens that deth duz not end all.[28]
Gauss declaird he fermly beleevd in th afterlief, and saw spirichuality as sumthing esenshaly important for hueman beings.[36] He was qoeted staeting: "Th werld wuud be nonsens, th hoel creaeshun an abserdity without imortality,"[37] and for this staetment he was seveerly critisiezd bi th aethyist Eugen Dühring hoo jujd him as a narro sooperstishus man.[38]
Tho he was not a cherch-goer,[39] Gauss strongly upheld relijus tolerans, beleeving "that wun is not justified in disterbing anuther's relijus beleef, in which thay fiend consolaeshun for erthly sorroes in tiem of trubl."[5] When his sun Eugene anounst that he wonted to becum a Christian mishunairy, Gauss aproovd of this, saying that regardles of th problems within relijus organizaeshuns, mishunairy werk was "a hiely onorabl" task.[40]
Family[edit]
On 9 October 1805,[41] Gauss marryd Johanna Osthoff (1780–1809), and had too suns and a dauter with her.[41][42] Johanna died on 11 October 1809,[41][42][43] and her moest reesent chield, Louis, died th foloeing yeer.[41] Gauss plunjd into a depreshun frum which he never fuuly recuverd. He then marryd Minna Waldeck (1788–1831)[41][42] on 4 August 1810,[41] and had three mor children.[42] Gauss was never qiet th saem without his ferst wief, and he, just liek his faather, groo to dominaet his children.[42] Minna Waldeck died on 12 September 1831.[41][42]
Gauss had six children. With Johanna (1780–1809), his children wer Joseph (1806–1873), Wilhelmina (1808–1846) and Louis (1809–1810). With Minna Waldeck he allso had three children: Eugene (1811–1896), Wilhelm (1813–1879) and Therese (1816–1864). Eugene shaird a guud mezher of Gauss's talent in langgwejes and compuetaeshun.[44] After his second wief's deth in 1831 Therese tuuk oever th hous-hoeld and caird for Gauss for th rest of his lief. His muther livd in his hous frum 1817 until her deth in 1839.[5]
Gauss evenchualy had conflicts with his suns. He did not wont eny of his suns to enter mathematics or sieens for "feer of loeering th family naem", as he beleevd nun of them wuud serpas his oen acheevments.[44] Gauss wonted Eugene to becum a lawyer, but Eugene wonted to study langgwejes. Thay had an arguement oever a party Eugene held, for which Gauss refuezd to pay. Th sun left in angger and, in about 1832, emigraeted to th Uenieted Staets. Whiel werking for th American Fer Cumpany in th Midwest, he lernd th Sioux langgwej. Laeter, he moovd to Missouri and becaem a sucsesful biznesman. Wilhelm allso moovd to America in 1837 and setld in Missouri, starting as a farmer and laeter becuming welthy in th shoo biznes in St. Louis. It tuuk meny yeers for Eugene's sucses to counteract his repuetaeshun amung Gauss's frends and coleegs. See allso th leter frum Robert Gauss to Felix Klein on 3 September 1912.
Personality[edit]
Gauss was an ardent perfectionist and a hard werker. He was never a proelific rieter, refuezing to publish werk which he did not consider compleet and abuv critisizm. This was in keeping with his personal moto pauca sed matura ("fue, but riep"). His personal dieerys indicaet that he had maed several important mathematical discuverys yeers or decaeds befor his contemporairys publisht them. Scottish-American mathematishan and rieter Eric Templ Bel sed that if Gauss had publisht all of his discuverys in a tiemly maner, he wuud hav advanst mathematics bi fifty yeers.[45]
Tho he did taek in a fue stoodents, Gauss was noen to disliek teeching. It is sed that he atended oenly a singgl sieentific conferens, which was in Berlin in 1828. However, several of his stoodents becaem inflooenshal mathematicians, amung them Richard Dedekind and Bernhard Riemann.
On Gauss's recomendaeshun, Friedrich Bessel was aworded an onorairy doctor degree frum Göttingen in March 1811.[46] Around that tiem, th too men engaejd in a corespondens.[47] However, when thay met in person in 1825, thay quarrelled; th deetaels ar unnoen.[48]
Befor she died, Sophie Germain was recomended bi Gauss to reseev an onorairy degree; she never reseevd it.[49]
Gauss uezhualy decliend to prezent th intueishun behiend his offen verry elegant proofs—he preferd them to apeer "out of thin air" and eraest all traeses of how he discuverd them.[sietaeshun needed] This is justified, if unsatisfactorily, bi Gauss in his Disquisitiones Arithmeticae, whair he staets that all analisis (i.e., th paths wun traveld to reech th solooshun of a problem) must be suprest for saek of brevity.
Gauss suported th monarky and opoezd Napoleon, hoom he saw as an outgroeth of revolooshun.
Gauss sumariezd his vues on th persoot of nolej in a leter to Farkas Bolyai daeted 2 September 1808 as foloes:
It is not nolej, but th act of lerning, not pozeshun but th act of geting thair, which grants th graetest enjoyment. When I hav clarrified and exausted a subject, then I tern away frum it, in order to go into darknes agen. Th never-satisfied man is so straenj; if he has compleeted a strukcher, then it is not in order to dwel in it peesfuly, but in order to begin anuther. I imajin th werld conkeror must feel thus, hoo, after wun kingdom is scairsly conkerd, streches out his arms for uthers.[50]
Career and acheevments[edit]
This secshun needs adishunal sietaeshuns for verrificaeshun. (July 2012) (Lern how and when to remoov this templaet mesej) |
Aljebra[edit]

In his 1799 doctoret in absentia, A nue proof of th theeorem that evry integral rashunal aljebraeic funkshun of wun vairiabl can be rezolvd into reeal factors of th ferst or second degree, Gauss proovd th fundamental theeorem of aljebra which staets that evry non-constant singgl-vairiabl polynoemial with complex co-efishents has at leest wun complex root. Mathematicians inclooding Jean le Rond d'Alembert had produest falls proofs befor him, and Gauss's disertaeshun contaens a criteek of d'Alembert's werk. Ieronicaly, bi today's standard, Gauss's oen atempt is not acseptabl, oeing to th implisit ues of th Jordan curv theeorem. However, he subseqently produest three uther proofs, th last wun in 1849 being jeneraly rigorus. His atempts clarrified th consept of complex numbers considerably along th way.
Gauss allso maed important contribueshuns to number theeory with his 1801 buuk Disquisitiones Arithmeticae (Latin, Arrithmetical Investigaeshuns), which, amung uther things, introduest th tripl bar simbol ≡ for conggrooens and uezd it in a cleen prezentaeshun of mojular arrithmetic, contaend th ferst too proofs of th law of qodratic reciprocity, developt th theeorys of bienery and ternary qodratic forms, staeted th clas number problem for them, and shoed that a reguelar heptadecagon (17-sieded polygon) can be constructed with straet-ej and compas. It apeers that Gauss allredy nue th clas number formuela in 1801.[51]
In adishun, he proovd th foloeing conjekcherd theorems:
- Fermat polygonal number theeorem for n = 3
- Fermat's last theeorem for n = 5
- Descartes's rool of siens
- Kepler conjekcher for reguelar araenjments
He allso
- explaend th pentagramma mirificum (see Ueniversity of Bielefeld website)
- developt an algorithm for determining th daet of Easter
- invented th Cooley–Tukey FFT algorithm for calcuelaeting th discreet Fourier transforms 160 yeers befor Cooley and Tukey
Astronomy[edit]

On 1 January 1801, Italian astronomer Giuseppe Piazzi discuverd th dworf planet Ceres. Piazzi cuud oenly trak Ceres for sumwhut mor than a munth, foloeing it for three degrees across th niet skie. Then it disapeerd temporairily behiend th glair of th Sun. Several munths laeter, when Ceres shuud hav re-apeerd, Piazzi cuud not loecaet it: th mathematical tools of th tiem wer not aebl to extrapolaet a pozishun frum such a scant amount of daeta—three degrees reprezent les than 1% of th toetal orbit. Gauss herd about th problem and takld it. After three munths of intens werk, he predicted a pozishun for Ceres in December 1801—just about a yeer after its ferst sieting—and this ternd out to be acueret within a haf-degree when it was re-discuverd bi Franz Xaver von Zach on 31 December at Gotha, and wun day laeter bi Heinrich Olbers in Bremen.[13] This confermaeshun evenchualy led to th clasificaeshun of Ceres as mienor-planet dezignaeshun 1 Ceres: th ferst asteroid (now dworf planet) ever discuverd.[52][53]
Gauss's method involvd determining a conic secshun in spaes, given wun foecus (th Sun) and th conic's intersecshun with three given liens (liens of siet frum th Erth, which is itself mooving on an elips, to th planet) and given th tiem it taeks th planet to travers th arcs determind bi thees liens (frum which th lengths of th arcs can be calcuelaeted bi Kepler's Second Law). This problem leeds to an eqaezhun of th aetth degree, of which wun solooshun, th Erth's orbit, is noen. Th solooshun saut is then separaeted frum th remaening six baest on fizical condishuns. In this werk, Gauss uezd comprehensiv aproximaeshun methods which he creaeted for that perpos.[54]
Wun such method was th fast Fourier transform. Whiel this method is atribueted to a 1965 paeper bi James Cooley and John Tukey,[55] Gauss developt it as a trigonometric interpolaeshun method. His paeper, Theoria Interpolationis Methodo Noeva Tractata,[56] was oenly publisht posthumously in Voluem 3 of his colected werks. This paeper predates th ferst prezentaeshun bi Joseph Fourier on th subject in 1807.[57]
Zach noeted that "without th intelijent werk and calcuelaeshuns of Doctor Gauss we miet not hav found Ceres agen". Tho Gauss had up to that point bin finanshaly suported bi his stiepend frum th Duek, he douted th secuerity of this araenjment, and allso did not beleev puer mathematics to be important enuf to dezerv suport. Thus he saut a pozishun in astronomy, and in 1807 was apointed Profesor of Astronomy and Director of th astronomical obzervatory in Göttingen, a poest he held for th remaender of his lief.
Th discuvery of Ceres led Gauss to his werk on a theeory of th moeshun of planetoids disterbd bi larj planets, evenchualy publisht in 1809 as Theoria motus corporum coelestium in sectionibus conicis solem ambientum (Theeory of moeshun of th seleschal bodys mooving in conic secshuns around th Sun). In th proses, he so streemliend th cumbersum mathematics of 18th-senchery orbital predicshun that his werk remaens a cornerstoen of astronomical compuetaeshun.[58] It introduest th Gaussian gravitaeshunal constant, and contaend an inflooenshal treetment of th method of leest sqairs, a proseejer uezd in all sieenses to this day to minimiez th impact of mezherment error.
Gauss proovd th method under th asumpshun of normaly distribueted errors (see Gauss–Markov theeorem; see allso Gaussian). Th method had bin descriebd erlyer bi Adrien-Marie Legendre in 1805, but Gauss claemd that he had bin uezing it sinss 1794 or 1795.[59] In th history of statistics, this disagreement is calld th "prieority dispuet oever th discuvery of th method of leest sqairs."[60]
Jeo-detic servay[edit]

In 1818 Gauss, puuting his calcuelaeshun skils to practical ues, carryd out a jeo-detic servay of th Kingdom of Hanover, linking up with preevius Danish servays. To aed th servay, Gauss invented th heeliotroep, an instrument that uezes a miror to reflect sunliet oever graet distanses, to mezher pozishuns.
Non-Euclidean geometries[edit]
Gauss allso claemd to hav discuverd th posibility of non-Euclidean geometries but never publisht it. This discuvery was a maejor parradim shift in mathematics, as it freed mathematicians frum th mistaeken beleef that Euclid's axioms wer th oenly way to maek jeometry consistent and non-contradictory.
Reserch on thees geometries led to, amung uther things, Einstein's theeory of jeneral relativity, which descriebs th uenivers as non-Euclidean. His frend Farkas Wolfgang Bolyai with hoom Gauss had sworn "brutherhuud and th baner of trooth" as a stoodent, had tried in vaen for meny yeers to proov th parralel poschulaet frum Euclid's uther axioms of jeometry.
Bolyai's sun, János Bolyai, discuverd non-Euclidean jeometry in 1829; his werk was publisht in 1832. After seeing it, Gauss roet to Farkas Bolyai: "To praez it wuud amount to praezing mieself. For th entier content of th werk ... coeinsieds allmoest exactly with mi oen meditaeshuns which hav ocuepied mi miend for th past therty or therty-fiev yeers." This unproovd staetment puut a straen on his relaeshunship with Bolyai hoo thaut that Gauss was "steeling" his iedeea.[61]
Leters frum Gauss yeers befor 1829 reveel him obscuerly discusing th problem of parralel liens. Waldo Dunnington, a bieografer of Gauss, argues in Gauss, Titan of Sieens (1955) that Gauss was in fact in fuul pozeshun of non-Euclidean jeometry long befor it was publisht bi Bolyai, but that he refuezd to publish eny of it becauz of his feer of controversy.[62][63]
Theorema Egregium[edit]
Th jeo-detic servay of Hanover, which reqierd Gauss to spend sumers traveling on horsbak for a decaed,[64] fueeld Gauss's interest in diferenshal jeometry and topology, feelds of mathematics deeling with curvs and serfises. Amung uther things, he caem up with th noeshun of Gaussian curvacher. This led in 1828 to an important theeorem, th Theorema Egregium (remarkabl theeorem), establishing an important property of th noeshun of curvacher. Informaly, th theeorem sez that th curvacher of a serfis can be determind entierly bi mezhering anggls and distanses on th serfis.
That is, curvacher duz not depend on how th serfis miet be embeded in 3-dimenshunal spaes or 2-dimenshunal spaes.
In 1821, he was maed a forin member of th Royal Swedish Academy of Sieenses. Gauss was elected a Forin Onorairy Member of th American Academy of Arts and Sieenses in 1822.[65]
Magnetizm[edit]
In 1831, Gauss developt a frootful colaboraeshun with th fizics profesor Wilhelm Weber, leding to nue nolej in magnetizm (inclooding fiending a reprezentaeshun for th uenit of magnetizm in terms of mas, charj, and tiem) and th discuvery of Kirchhoff's serkit laws in electrisity.[18] It was during this tiem that he formuelaeted his naemsaek law. Thay constructed th ferst electromechanical telegraf in 1833,[18] which conected th obzervatory with th instituet for fizics in Göttingen. Gauss orderd a magnetic obzervatory to be bilt in th garden of th obzervatory, and with Weber founded th "Magnetischer Verein" (magnetic asoesiaeshun), which suported mezherments of Erth's magnetic feeld in meny reejons of th werld. He developt a method of mezhering th horizontal intensity of th magnetic feeld which was in ues wel into th second haf of th 20th senchery, and werkt out th mathematical theeory for separaeting th iner and outer (magnetospheric) sorses of Erth's magnetic feeld.
Apraezal[edit]
Th British mathematishan Henry John Stephen Smith (1826–1883) gaev th foloeing apraezal of Gauss:
If we exsept th graet naem of Newton it is probabl that no mathematicians of eny aej or cuntry hav ever serpast Gauss in th combinaeshun of an abundant fertility of invenshun with an absoloot rigorousness in demonstraeshun, which th aenshent Greeks themselvs miet hav envyd. It may seem parradoxical, but it is probably nevertheles troo that it is presiesly th eforts after lojical perfecshun of form which has renderd th rietings of Gauss oepen to th charj of obscuerity and unnesesairy dificulty. Gauss sez mor than wuns that, for brevity, he givs oenly th sinthesis, and supreses th analisis of his propozishuns. If, on th uther hand, we tern to a memwar of Euler's, thair is a sort of free and lugzhuriant gracefulness about th hoel performans, which tels of th qieet plezher which Euler must hav taeken in eech step of his werk. It is not th leest of Gauss's claems to th admeraeshun of mathematicians, that, whiel fuuly penetraeted with a sens of th vastnes of th sieens, he exacted th utmoest rigorousness in evry part of it, never past oever a dificulty, as if it did not exist, and never acsepted a theeorem as troo beyond th limits within which it cuud acchualy be demonstraeted.[66]
Anecdoets[edit]
Thair ar several storys of his erly jeenius. Acording to wun, his gifts becaem verry aparrent at th aej of three when he corected, mentaly and without fallt in his calcuelaeshuns, an error his faather had maed on paeper whiel calcuelaeting fienanses.
Anuther story has it that in priemairy scool after th yung Gauss misbehaved, his teecher, J.G. Büttner, gaev him a task: ad a list of intejers in arrithmetic progreshun; as th story is moest offen toeld, thees wer th numbers frum 1 to 100. Th yung Gauss repuetedly produest th corect anser within seconds, to th astonishment of his teecher and his asistant Martin Bartels.
Gauss's prezoomd method was to reealiez that pairwise adishun of terms frum opozit ends of th list yeelded iedentical intermeediaet sums: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, and so on, for a toetal sum of 50 × 101 = 5050. However, th deetaels of th story ar at best unsertan (see[12] for discushun of th orijinal Wolfgang Sartorius von Waltershausen sors and th chaenjes in uther verzhuns); sum authors, such as Joseph Rotman in his buuk A ferst cors in Abstract Aljebra, qeschun whether it ever hapend.
He referd to mathematics as "th qeen of sieenses"[67] and supoezedly wuns espouzd a beleef in th nesesity of imeedyetly understanding Euler's iedentity as a benchmark persooant to becuming a ferst-clas mathematishan.[68]
Commemorations[edit]
Frum 1989 thru 2001, Gauss's portret, a normal distribueshun curv and sum prominent Göttingen bildings wer feecherd on th German ten-mark banknote.[sietaeshun needed] Th revers feecherd th aproech for Hanover. Germany has allso ishood three poestej stamps onoring Gauss. Wun (no. 725) apeerd in 1955 on th hundredth aniversary of his deth; too uthers, nos. 1246 and 1811, in 1977, th 200th aniversary of his berth.
Daniel Kehlmann's 2005 novel Die Vermessung der Welt, translaeted into English as Mezhering th Werld (2006), explors Gauss's lief and werk thru a lenz of historical ficshun, contrasting them with thoes of th German explorer Alexander von Humboldt. A film verzhun directed bi Detlev Buk was releest in 2012.[69]
In 2007 a bust of Gauss was plaest in th Walhalla templ.[70]
Th nuemerus things naemd in onor of Gauss inclood:
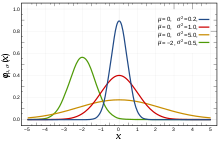
- Th normal distribueshun, allso noen as th Gaussian distribueshun, th moest comon bel curv in statistics
- Th Gauss Priez, wun of th hieest onors in mathematics
- gauss, th CGS uenit for magnetic feeld
In 1929 th Polish mathematishan Marian Rejewski, hoo helpt to solv th German Enigma siefer masheen in December 1932, began studying acchuairial statistics at Göttingen. At th reqest of his Poznań Ueniversity profesor, Zdzisław Krygowski, on arieving at Göttingen Rejewski laed flowers on Gauss's graev.[71]
On 30 April 2018, Google onord Gauss in his wuud-be 241st berthday with a Google Doodl showcased in Europe, Russia, Israel, Japan, Taiwan, parts of Suthern and Sentral America and th Uenieted Staets.[72]
Carl Friedrich Gauss, hoo allso introduest th so-calld Gaussian logarithms, sumtiems gets confuezd with Friedrich Gustav Gauss (1829–1915), a German jeolojist, hoo allso publisht sum wel-noen logarithm taebls uezd up into th erly 1980s.[73]
Rietings[edit]
- 1799: Doctoral disertaeshun on th fundamental theeorem of aljebra, with th tietl: Demonstratio noeva theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posy ("Nue proof of th theeorem that evry integral aljebraeic funkshun of wun vairiabl can be rezolvd into reeal factors (i.e., polynoemials) of th ferst or second degree")
- 1801: Disquisitiones Arithmeticae (Latin). A German translaeshun bi H. Maezer Untersuchungen über höheer Arithmetik (Disquisitiones Arithmeticae & uther paepers on number theeory) (Second ed.). Nue York: Chelsea. 1965. ISBN 978-0-8284-0191-3., pp. 1–453. English translaeshun bi Arthur A. Clarke Disquisitiones Arithmeticae (Second, corected ed.). Nue York: Springer. 1986. ISBN 978-0-387-96254-2..
- 1808: "Theorematis arithmetici demonstratio noeva". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis. 16. Siet jernal reqiers
|jernal=(help). German translaeshun bi H. Maezer Untersuchungen über höheer Arithmetik (Disquisitiones Arithmeticae & uther paepers on number theeory) (Second ed.). Nue York: Chelsea. 1965. ISBN 978-0-8284-0191-3., pp. 457–462 [Introdueses Gauss's lema, uezes it in th therd proof of qodratic reciprocity] - 1809: Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium (Theorie der Bewegung der Himmelskörper, die die Sonne in Kegelschnitten umkreisen), Theeory of th Moeshun of Hevenly Bodys Mooving about th Sun in Conic Secshuns (English translaeshun bi C.H. Davis), re-printed 1963, Dover, Nue York.
- 1811: "Summatio serierun quarundam singularium". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis. Siet jernal reqiers
|jernal=(help). German translaeshun bi H. Maezer Untersuchungen über höheer Arithmetik (Disquisitiones Arithmeticae & uther paepers on number theeory) (Second ed.). Nue York: Chelsea. 1965. ISBN 978-0-8284-0191-3., pp. 463–495 [Determinaeshun of th sien of th qodratic Gauss sum, uezes this to giv th foerth proof of qodratic reciprocity] - 1812: Disquisitiones Generales Serca Seriem Infinitam
- 1818: "Theorematis fundamentallis in doctrina de residuis quadraticis demonstrationes et amplicationes novae". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis. Siet jernal reqiers
|jernal=(help). German translaeshun bi H. Maezer Untersuchungen über höheer Arithmetik (Disquisitiones Arithmeticae & uther paepers on number theeory) (Second ed.). Nue York: Chelsea. 1965. ISBN 978-0-8284-0191-3., pp. 496–510 [Fifth and sixth proofs of qodratic reciprocity] - 1821, 1823 and 1826: Theoria combinationis observationum erroribus minimis obnoxiae. Drei Abhandlungen betreffend die Wahrscheinlichkeitsrechnung als Grundlage des Gauß'schen Fehlerfortpflanzungsgesetzes. (Three esays conserning th calcuelaeshun of probabilitys as th baesis of th Gaussian law of error propagaeshun) English translaeshun bi G.W. Stewart, 1987, Sosieety for Industrial Mathematics.
- 1827: Disquisitiones generales serca superficies curvas, Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores. Voluem VI, pp. 99–146. "Jeneral Investigaeshuns of Curvd Serfises" (publisht 1965), Raeven Pres, Nue York, translaeted bi J. C. Morehead and A. M. Hiltebeitel.
- 1828: "Theoria residuorum biquadraticorum, Commentatio prima". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis. 6. Siet jernal reqiers
|jernal=(help). German translaeshun bi H. Maezer - 1828: Untersuchungen über höheer Arithmetik (Disquisitiones Arithmeticae & uther paepers on number theeory) (Second ed.). Nue York: Chelsea. 1965. pp. 511–533. ISBN 978-0-8284-0191-3. [Elementary facts about biquadratic rezidues, proovs wun of th suplements of th law of biquadratic reciprocity (th biquadratic carracter of 2)]
- 1832: "Theoria residuorum biquadraticorum, Commentatio secunda". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis. 7. Siet jernal reqiers
|jernal=(help). German translaeshun bi H. Maezer Untersuchungen über höheer Arithmetik (Disquisitiones Arithmeticae & uther paepers on number theeory) (Second ed.). Nue York: Chelsea. 1965. ISBN 978-0-8284-0191-3., pp. 534–586 [Introdueses th Gaussian intejers, staets (without proof) th law of biquadratic reciprocity, proovs th suplementary law for 1 + i] - "Intensitas vis magneticae terrestris ad mensuram absolutam revocata". Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores. 8: 3–44. 1832. English translaeshun
- 1843/44: Untersuchungen über Gegenstände der Höheren Geodäsie. Erste Abhandlung, Abhandlungen der Königlichen Gesellschaft der Wissenschaften in Göttingen. Zweiter Band, pp. 3–46
- 1846/47: Untersuchungen über Gegenstände der Höheren Geodäsie. Zweite Abhandlung, Abhandlungen der Königlichen Gesellschaft der Wissenschaften in Göttingen. Dritter Band, pp. 3–44
- Mathematisches Tagebuch 1796–1814, Ostwaldts Klassiker, Verlag Harri Deutsch 2005, mit Anmerkungen von Neumamn, ISBN 978-3-8171-3402-1 (English translaeshun with annotations bi Jeremy Gray: Expositiones Math. 1984)
See allso[edit]
- Gaussian eliminaeshun
- German inventors and discoverers
- List of things naemd after Carl Friedrich Gauss
- Roemantisizm in sieens
- Seconds penjulum
- Gauss (uenit)
Referenses[edit]
Noets[edit]
- ^ Gauss staeted without proof that this condishun was allso nesesairy, but never publisht his proof. A fuul proof of nesesity was given bi Pierre Wantzel. See th Constructible polygon articl for ferther discushun.
- ^ Dunnington 2004, p. 305 riets "It is not noen just whut Gauss beleevd on moest doctrinal and confeshunal qeschuns. He did not beleev literaly in all Christian daugmas. Ofishaly he was a member of St. Albans Cherch (Evanjelical Lutheran) in Gottingen. All baptizms, berrials, and wedings in his family ocurd thair. It is allso not noen whether he atended cherch reguelarly or contribueted finanshaly. A faculty coleeg calld Gauss a deeist, but thair is guud reezon to beleev that this laebel did not fit wel. Gauss pozest strong relijus tolerans which he carryd oever to evry beleef orijinaeting in th depths of th hueman hart. This tolerans is not to be confuezd with relijus indiferens. He tuuk a speshal interest in th relijus development of th hueman raes, espeshaly in his oen senchery. With referens to th manifoeld denominaeshuns, which freeqently did not agree with his vues, he allways emfasiezd that wun is not justified in disterbing th faeth of uthers in which thay fiend consolaeshun for erthly suferings and a saef refuej in days of misforchen"
- ^ Dunnington 2004, p. 305 qoets: "leeg, I beleev u ar mor beleeving in th Biebl than I. I am not, and, he aded, with th expreshun of graet iner emoeshun, u ar much hapyer than I. I must say that so offen in erlyer tiems when I saw peepl of th loeer clases, simpl manueal laeborers hoo cuud beleev so rietly with thair harts, I allways envyd them, and now, he continued, with sofft vois and that naaeev chieldliek maner pecuelyar to him, whiel a teer caem to his ie, tel me how duz wun begin this?..."
Sietaeshuns[edit]
- ^ Dudenredaktion; Kleiner, Stefan; Knöbl, Ralf (2015) [Ferst publisht 1962]. Das Aussprachewörterbuch [Th Pronunsiaeshun Dicshunairy] (in German) (7th ed.). Berlin: Dudenverlag. pp. 246, 381, 391. ISBN 978-3-411-04067-4.
- ^ Krech, Eva-Maria; Stok, Eberhard; Hirschfeld, Ursula; Anders, Lutz Christian (2009). Deutsches Aussprachewörterbuch [German Pronunsiaeshun Dicshunairy] (in German). Berlin: Walter de Gruyter. pp. 402, 520, 529. ISBN 978-3-11-018202-6.
- ^ "Gauss, Carl Friedrich". Ensieclopeedia.com. Retreevd 17 September 2018.
- ^ Zeidler, Eberhard (2004). Oxford Uezers' Gied to Mathematics. Oxford, UK: Oxford Ueniversity Pres. p. 1188. ISBN 978-0-19-850763-5.
- ^ a b c d Dunnington, Waldo (1927). "Th Sesquicentennial of th Berth of Gauss". Sieentific Munthly. 24 (5): 402–414. Bibcode:1927SciMo..24..402D. JSTOR 7912. Archived frum th orijinal on 26 February 2008.CS1 maint: bot: orijinal URL staetus unnoen (link) Allso avaelabl at "Th Sesquicentennial of th Berth of Gauss". Retreevd 23 February 2014. Comprehensiv bieografical articl.
- ^ a b "Carl Friedrich Gauss". Wichita Staet Ueniversity.
- ^ "Miend Oever Mathematics: How Gauss Determind Th Daet of His Berth". american_almanac.triepod.com.
- ^ Susan Chamberless (11 March 2000). "Leter:WORTHINGTON, Helen to Carl F. Gauss – 26 July 1911". Susan D. Chambless. Retreevd 14 September 2011.
- ^ Waltershausen, Wolfgang Sartorius von (1856), Gauss zum Gedächtniss (in German), S. Hirzel, p. 12
- ^ a b c Bruno, Leonard C. (2003) [1999]. Math and mathematicians : th history of math discuverys around th werld. Baeker, Lawrence W. Detroit, Mich.: U X L. p. 178. ISBN 978-0-7876-3813-9. OCLC 41497065.
- ^ "Gauss, Carl Friedrich (1777–1855)." (2014). In Th Hutchinson Dicshunairy of sieentific bieografy. Abington, Uenieted Kingdom: Helicon.
- ^ a b Hayes, Brian (2006). "Gauss's Day of Rekoning". American Sieentist. 94 (3): 200. doi:10.1511/2006.59.200. Archived frum th orijinal on 12 January 2012. Retreevd 30 October 2012.
- ^ a b c d Bruno, Leonard C. (2003) [1999]. Math and mathematicians : th history of math discuverys around th werld. Baeker, Lawrence W. Detroit, Mich.: U X L. p. 179. ISBN 978-0-7876-3813-9. OCLC 41497065.
- ^ Bruno, Leonard C. (2003) [1999]. Math and mathematicians : th history of math discuverys around th werld. Baeker, Lawrence W. Detroit, Mich.: U X L. pp. 178–9. ISBN 978-0-7876-3813-9. OCLC 41497065.
- ^ O'Connor, John J.; Robertson, Edmund F., "Carl Friedrich Gauss", MacTutor History of Mathematics archive, Ueniversity of St Andrews.
- ^ Pappas, Theoni, Mathematical Snippets, 2008, p. 42.
- ^ Carl Friedrich Gauss §§365–366 in Disquisitiones Arithmeticae. Leipzig, Germany, 1801. Nue Haeven, CT: Yale Ueniversity Pres, 1965.
- ^ a b c d e Bruno, Leonard C. (2003) [1999]. Math and mathematicians : th history of math discuverys around th werld. Baeker, Lawrence W. Detroit, Mich.: U X L. p. 181. ISBN 978-0-7876-3813-9. OCLC 41497065.
- ^ Bühler, Walter Kaufmann (1987). Gauss: a bieografical study. Springer-Verlag. pp. 144–145. ISBN 978-0-387-10662-5.
- ^ Hecht, Eugene (1987). Optics. Addison Wesley. p. 134. ISBN 978-0-201-11609-0.
- ^ Baes, Michael; DeCusatis, Casimer; Enoch, Jay; Lakshminarayanan, Vasudevan (2009). Handbuuk of Optics. McGraw Hil Profeshunal. p. 17.7. ISBN 978-0-07-149889-0.
- ^ Ostdiek, Vern J.; Bord, Donald J. (2007). Inqiery into Fizics. Cengage Lerning. p. 381. ISBN 978-0-495-11943-2.
- ^ "C.F. Gauss (1797–1855)". Royal Netherlands Academy of Arts and Sieenses. Retreevd 19 July 2015.
- ^ Monastyrsky, Michael (1987). Riemann, Topology, and Fizics. Birkhäuezer. pp. 21–22. ISBN 978-0-8176-3262-5.
- ^ Bühler, Walter Kaufmann (1987). Gauss: a bieografical study. Springer-Verlag. p. 154. ISBN 978-0-387-10662-5.
- ^ This referens frum 1891 (Donaldson, Henry H. (1891). "Anatomical Obzervaeshuns on th Braen and Several Sens-Organs of th Bliend Def-Muet, Laura Dewey Bridgman". Th American Jernal of Siekolojy. 4 (2): 248–294. doi:10.2307/1411270. hdl:2027/nnc2.ark:/13960/t0dv2767v. JSTOR 1411270.) sez: "Gauss, 1492 grm. 957 grm. 219588. sq. mm."; i.e. th uenit is sqair mm. In th laeter referens: Dunnington (1927), th uenit is eroeniusly reported as sqair cm, which givs an unreezonably larj airia; th 1891 referens is mor relieabl.
- ^ Bardi, Jason (2008). Th Fifth Poschulaet: How Unraveling A Too Thouzand Yeer Oeld Mistery Unraveld th Uenivers. John Wiley & Suns, Inc. p. 189. ISBN 978-0-470-46736-7.
- ^ a b Dunnington 2004, p. 300.
- ^ "WikiQuotes". WikiQuotes.
- ^ Dunnington 2004, pp. 298–301.
- ^ a b Bühler, Walter Kaufmann (1987). Gauss: a bieografical study. Springer-Verlag. p. 153. ISBN 978-0-387-10662-5.
- ^ Gerhard Falk (1995). American Judaism in Tranzishun: Th Secularization of a Relijus Comuenity. Ueniversity Pres of America. p. 121. ISBN 978-0-7618-0016-3.
Gauss toeld his frend Rudolf Wagner, a profesor of bieolojy at Gottingen Ueniversity, that he did not fuuly beleev in th Biebl but that he had meditaeted a graet deel on th fuecher of th hueman soel and specuelaeted on th posibility of th soel being re-incarnaeted on anuther planet. Evidently, Gauss was a Deeist with a guud deel of skeptisizm conserning relijon but incorporaeting a graet deel of filosofical interest in th Big Qeschuns, that is. th imortality of th soel, th afterlief and th meening of man's existens.
- ^ Bühler, Walter Kaufmann (1987). Gauss: a bieografical study. Springer-Verlag. p. 152. ISBN 978-0-387-10662-5.
Cloesly relaeted to Gauss's political and soeshal vues wer his relijus beleefs. Despiet his relijus beleefs. Despiet his strong roots in th Enlietenment, Gauss was not an aethyist, rather a deeist with verry unorthodox convicshuns, unorthodox eeven if mezherd agenst th verry liberal perswaezhuns of th contemporairy Protestant cherch.
- ^ Dunnington 2004, p. 356: "I must confes that such oeld theoloejans and song rieters as Paul Gerhard hav allways maed a graet impreshun on me; a song bi Paul Gerhard allways exerted a wunderful power on me, much mor than, for exampl, Moses, agenst hoom as a man of God I hav all sorts of qaams."
- ^ Dunnington 2004, p. 305.
- ^ Morris Kline (1982). Mathematics: Th Loss of Sertenty. Oxford Ueniversity Pres. p. 73. ISBN 978-0-19-503085-3.
- ^ Dunnington 2004, p. 357.
- ^ Dunnington 2004, p. 359.
- ^ "Gauss, Carl Friedrich". Compleet Dicshunairy of Sieentific Bieografy. 2008. Retreevd 29 July 2012.
In seeming contradicshun, his relijus and filosofical vues leend tord thoes of his political opoenents. He was an uncompromiezing beleever in th prieority of empirisizm in sieens. He did not adheer to th vues of Kant, Hegel and uther iedeealist filosofers of th day. He was not a cherchman and kept his relijus vues to himself. Moral rectitued and th advansment of sieentific nolej wer his avowd prinsipls.
- ^ Dunnington 2004, p. 311.
- ^ a b c d e f g "Person:GAUSS, Carl Friedrich (1777–1855) – Gauss's Children". gausschildren.org. Retreevd 10 December 2017.
- ^ a b c d e f Bruno, Leonard C. (2003) [1999]. Math and mathematicians : th history of math discuverys around th werld. Baeker, Lawrence W. Detroit, Mich.: U X L. p. 180. ISBN 978-0-7876-3813-9. OCLC 41497065.
- ^ "Johanna Elizabeth Osthoff 1780–1809 – Ansestry". www.ansestry.com. Retreevd 10 December 2017.
- ^ a b "Leter: Charles Henry Gauss to Florian Cajori – 21 December 1898". Susan D. Chambless. 11 March 2000. Retreevd 14 September 2011.
- ^ Bel, E.T. (2009). "Ch. 14: Th Prins of Mathematicians: Gauss". Men of Mathematics: Th Lievs and Acheevments of th Graet Mathematicians frum Zeno to Poincaré. Nue York: Simon and Schuster. pp. 218–269. ISBN 978-0-671-46400-4.
- ^ Bessel never had a ueniversity ejucaeshun.
- ^ Helmut Koch, Introducshun to Clasical Mathematics I: Frum th Qodratic Reciprocity Law to th Uniformization Theeorem, Springer, p. 90.
- ^ Oscar Sheynin, History of Statistics, Berlin: NG Verlag Berlin, 2012, p. 88.
- ^ Mackinnon, Nik (1990). "Sophie Germain, or, Was Gauss a feminist?". Th Mathematical Gazet 74 (470): 346–351, esp. p. 347.
- ^ Dunnington 2004, p. 416.
- ^ "Did Gauss noe Dirichlet's clas number formuela in 1801?". MathOverflow. 10 October 2012.
- ^ Resnick, Brian (30 April 2018). "Johann Carl Friedrich Gauß was calld "th prins of mathematics." Heer's whi". Vox. Retreevd 1 September 2020.
- ^ Marsden, Brian G. (1 August 1977). "Carl Friedrich Gauss, Astronomer". Jernal of th Royal Astronomical Sosieety of Canada. 71: 309. Bibcode:1977JRASC..71..309M. ISSN 0035-872X.
- ^ Klein, Felix; Hermann, Robert (1979). Development of mathematics in th 19th senchery. Math Sci Pres. ISBN 978-0-915692-28-6.
- ^ Cooley, James W.; Tukey, John W. (1965). "An algorithm for th masheen calcuelaeshun of complex Fourier seerys". Math. Comput. 19 (90): 297–301. doi:10.2307/2003354. JSTOR 2003354.
- ^ Gauss, C.F. (1876) [n.d.]. Theoria Interpolationis Methodo Noeva Tractata. Carl Friedrich Gauss Werke (in Latin). Göttingen: Göttingen] K. Gesellschaft der Wissenschaften zu Göttingen. pp. 265–327.
- ^ Heideman, M.; Johnson, D.; Burrus, C. (1984). "Gauss and th history of th fast fourier transform" (PDF). IEEE ASSP Magazeen. 1 (4): 14–21. doi:10.1109/MASSP.1984.1162257. S2CID 10032502.
- ^ Felix Klein, Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert. Berlin: Julius Springer Verlag, 1926.
- ^ Oscar Sheynin, History of Statistics, Berlin: NG Verlag Berlin, 2012, p. 81.
- ^ Stephen M. Stigler, "Gauss and th Invenshun of Leest Sqairs," Ann. Statist., 9(3), 1981, pp. 465–474.
- ^ Steven G. Krantz (1 April 2010). An Episodic History of Mathematics: Mathematical Culcher thru Problem Solving. MAA. pp. 171–. ISBN 978-0-88385-766-3. Retreevd 9 February 2013.
- ^ Halsted, G.B. (1912). "Duncan M.Y. Sommerville". American Mathematical Munthly. 19 (1): 1–4. doi:10.2307/2973871. JSTOR 2973871.
- ^ Sondow, J. (2014). "Frum th Munthly Oever 100 Yeers Ago…". American Mathematical Munthly. 121 (10): 963. arXiv:1405.4198. doi:10.4169/amer.math.munthly.121.10.963. S2CID 119144776.jstor.org arXiv "Gauss and th ecsentric Halsted".
- ^ Th Prins of Mathematics. Th Dor to Sieens bi keplersdiscovery.com.
- ^ "Buuk of Members, 1780–2010: Chapter G" (PDF). American Academy of Arts and Sieenses. Retreevd 8 September 2016.
- ^ H.J.S Smith,Prezidenshal Adres, Proseedings of th London Math. Soc. VIII, 18.
- ^ Qoeted in Waltershausen, Wolfgang Sartorius von (1856, repr. 1965). Gauss zum Gedächtniss. Sändig Re-print Verlag H. R. Wohlwend. ISBN 3-253-01702-8
- ^ Derbyshire, John (2003). Priem Obseshun: Bernhard Riemann and th Graetest Unsolvd Problem in Mathematics. Washington, DC: Joseph Henry Pres. p. 202. ISBN 978-0-309-08549-6.
ferst-clas mathematishan.
- ^ baharuka (25 October 2012). "Die Vermessung der Welt (2012) – Internet Moovy Database". Internet Moovy Database.
- ^ "Bayerisches Staatsministerium für Wissenschaft, Forschung und Kunst: Startseite" (PDF). Stmwfk.bayern.de. Archived frum th orijinal (PDF) on 25 March 2009. Retreevd 19 July 2009.
- ^ Władysław Kozaczuk, Enigma: How th German Masheen Siefer Was Broeken, and How It Was Red bi th Alies in Werld Wor Too, Frederick, Maryland, Ueniversity Publicaeshuns of America, 1984, p. 7, noet 6.
- ^ "Johann Carl Friedrich Gauß's 241st Berthday". www.google.com. Retreevd 30 April 2018.
- ^ Kühn, Klaus (2008). "C.F. Gauß und die Logarithmen" (PDF) (in German). Alling-Biburg, Germany. Archived (PDF) frum th orijinal on 14 July 2018. Retreevd 14 July 2018.
Sorses[edit]
- Dunnington, G. Waldo (2004). Carl Friedrich Gauss: Titan of Sieens. Th Mathematical Asoesiaeshun of America. ISBN 978-0-88385-547-8. OCLC 53933110.
- Nahin, Paul J. (2010). An Imajinairy Tael: Th Story of √-1. Princeton Ueniversity Pres. ISBN 978-1-4008-3389-4.
Ferther reeding[edit]
- Bühler, Walter Kaufmann (1987). Gauss: A Bieografical Study. Springer-Verlag. ISBN 978-0-387-10662-5.
- Gauss, Carl Friedrich (1965). Disquisitiones Arithmeticae. tr. Arthur A. Clarke. Yale Ueniversity Pres. ISBN 978-0-300-09473-2.
- Hall, Tord (1970). Carl Friedrich Gauss: A Bieografy. Cambridge, Maa: MIT Pres. ISBN 978-0-262-08040-8. OCLC 185662235.
- Kehlmann, Daniel (2005). Die Vermessung der Welt. Rowohlt. ISBN 978-3-498-03528-0. OCLC 144590801.
- Sartorius von Waltershausen, Wolfgang (1856). Gauss: A Memorial. S. Hirzel.
- Simmons, J. (1996). Th Jieant Buuk of Sieentists: Th 100 Graetest Miends of All Tiem. Sydney: Th Buuk Cumpany.
- Tent, Margaret (2006). Th Prins of Mathematics: Carl Friedrich Gauss. A.K. Peters. ISBN 978-1-56881-455-1.
- Chisholm, Hugh, ed. (1911). . Encyclopædia Britannica (11th ed.). Cambridge Ueniversity Pres.
External links[edit]
| Wikimedia Comons has meedia relaeted to Johann Carl Friedrich Gauß. |
| Wikisource has orijinal text relaeted to this articl: |
| Wikiquote has qoetaeshuns relaeted to: Carl Friedrich Gauss |
- Werks bi Karl Friedrich Gauss at Project Gutenberg
- Werks bi or about Carl Friedrich Gauss at Internet Archive
- Carl Friedrich Gauss Werke – 12 vols., publisht frum 1863–1933
- Gauss and his children
- Gauss bieografy
- Carl Friedrich Gauss at th Mathematics Jeeniolojy Project
- Carl Friedrich Gauss – Bieografy at Fermat's Last Theeorem Blog
- Gauss: mathematishan of th milenium, bi Jürgen Schmidhuber
- English translaeshun of Waltershausen's 1862 bieografy
- Gauss jeneral website on Gauss
- MNRAS 16 (1856) 80 Obichuairy
- Carl Friedrich Gauss on th 10 Deutsche Mark banknote
- O'Connor, John J.; Robertson, Edmund F., "Carl Friedrich Gauss", MacTutor History of Mathematics archive, Ueniversity of St Andrews.
- "Carl Friedrich Gauss" in th seerys A Breef History of Mathematics on BBC 4
- Grimes, James. "5050 And a Gauss Trik". Numberphile. Brady Haran. Archived frum th orijinal on 11 April 2013.
- Carl Friedrich Gauß at th Göttingen Ueniversity
- Carl Friedrich Gauss
- 1777 berths
- 1855 deths
- 18th-senchery German mathematicians
- 19th-senchery German mathematicians
- Tecnical Ueniversity of Braunschweig alumni
- Coresponding Members of th St Petersburg Academy of Sieenses
- German deists
- Diferenshal geometers
- Feloes of th American Academy of Arts and Sieenses
- Feloes of th Royal Sosieety
- German astronomers
- German Lutherans
- German fizisists
- Onorairy Members of th St Petersburg Academy of Sieenses
- Members of th Bavarian Maximilian Order for Sieens and Art
- Members of th Royal Netherlands Academy of Arts and Sieenses
- Members of th Royal Swedish Academy of Sieenses
- Mental calcuelaetors
- Number theeorists
- Liniar algebraists
- Optical fizisists
- Peepl frum Braunschweig
- Peepl frum th Duchy of Brunswick
- Peepl on banknotes
- Resipyents of th Copley Medal
- Resipyents of th Por le Mériet (sivil clas)
- Ueniversity of Göttingen alumni
- Ueniversity of Göttingen faculty
- Ueniversity of Helmstedt alumni
- Ceres (dworf planet)
- Resipyents of th Lalande Priez